LeetCode 885 螺旋矩阵 III
1 题目描述
在一个R行C列的二维网格上,我们起始在(r0, c0)位置,且面朝东。
这样,矩阵的西北角在第一行第一列,东南角在最后一行最后一列。
现在,我们以顺时针螺旋形状来访问网格的每个位置。
当走到网格边界之外时,则继续在边界之外走(可能稍后会回到网格的边界)。
最终,我们访问了全部R * C个空间。
返回一个代表网格访问顺序的列表。
注:
a)1 <= R <= 100
b)1 <= C <= 100
c)0 <= r0 < R
d)0 <= c0 < C
例子1:
输入:R = 1, C = 4, r0 = 0, c0 = 0
输出:[[0,0],[0,1],[0,2],[0,3]]
释义:
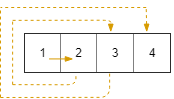
例子2:
输入:R = 5, C = 6, r0 = 1, c0 = 4
输出:[[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]
释义:
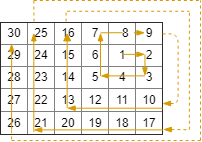
题目出处:LeetCode
2 解决思路
a)首先访问当前位置空间;
b)用circle表示当前访问到第几圈,从第1圈开始直至还有未触达的边界,即扩大圈半径进行如下循环:
i)首先walk方向为朝下,从i为max(0, r0-circle+1),j为c0 + circle开始,若j未跨过边界,则自上到下直至i抵达r0+circle的上一个空间或边界;
ii)然后walk方向为朝左,从i为r0 + circle,j为min(c-1, c0+circle)开始,若i未跨过边界,则自右到左直至j抵达c0-circle的上一个空间或边界;
iii)然后walk方向为朝上,从i为min(r-1, r0+circle),j为c0 - circle开始,若j未跨过边界,则自下到上直至i抵达r0-circle的上一个空间或边界;
iv)最后walk方向为朝右,从i为r0 - circle,j为max(0, c0-circle)开始,若i未跨过边界,则自左到右直至j抵达c0+circle或边界。
c)循环退出即遍历完了所有的空间。
3 Golang实现代码
https://github.com/leileiluoluo/
func min(a, b int) int {
if a < b {
return a
}
return b
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func spiralMatrixIII(r int, c int, r0 int, c0 int) [][]int {
walk := make([][]int, r*c)
i, j := r0, c0
index := 0
walk[index] = []int{i, j}
index++
circle := 1
for r0+circle < r || r0-circle >= 0 ||
c0+circle < c || c0-circle >= 0 {
// down direction
i = max(0, r0-circle+1)
j = c0 + circle
for j < c && i < r0+circle && i < r {
walk[index] = []int{i, j}
index++
i++
}
// left direction
i = r0 + circle
j = min(c-1, c0+circle)
for i < r && j > c0-circle && j >= 0 {
walk[index] = []int{i, j}
index++
j--
}
// up direction
i = min(r-1, r0+circle)
j = c0 - circle
for j >= 0 && i > r0-circle && i >= 0 {
walk[index] = []int{i, j}
index++
i--
}
// right direction
i = r0 - circle
j = max(0, c0-circle)
for i >= 0 && j <= c0+circle && j < c {
walk[index] = []int{i, j}
index++
j++
}
circle++
}
return walk
}
相关文章
评论
 正在加载评论......
正在加载评论......